Upline: Infos & Dokus Elektronik Regelungstechnik

Entwurf und Simulation von Regelkreisen

Es handelt sich bei diesem Dokument um ein Labor-Protokoll des Faches Regelungstechnik 2 im Studiengang Informationstechnik Vernetzte Systeme an der FHTW Berlin im Sommersemester 2006 bei Professor Dlabka.

Aufgabe 1.1 Sprungantwort der Regelstrecke

Schreiben Sie ein MATLAB-Skript, das die Sprungantwort der gegebenen Regelstrecke bestimmt. Das Programm soll außerdem automatisch die Ersatzparameter V, Tu und Tg mit dem Zweipunkte-Verfahren (bei 30% und 70%) bestimmen.
Als Ergebnis soll eine Figur vorliegen, in der die Sprungantwort und die Ersatzparameter angezeigt werden.
Gegeben: wd=0.2/s; V=2; T1=7s; T2=3s; T3=0.2s; T4=0.2s

Aufgabe 1.2 Bestimmung der Reglerparameter, Simulation des Regelkreises

Bestimmen Sie die Reglerparameter nach Kuhn für einen PID-T1-Regler:
Gr(p)=Vr(1+(1/(pTi)+pT/(1+pTr)
mit Vr=A/Vp, Ts=Tu+Tg, Ti=BTs, Td=CTs, Tr=0.3Td, A=1, B=0.66, C=1.67
Programmieren Sie mit SIMULINK einen Standard-Regelkreis mit den Blöcken „Transfer Fcn“ zur Aufnahme der Sprungantwort des Führungsverhaltens des Regelkreises. Erweitern Sie das MATLAB-Skript, so dass Sie SIMULINK aus MATLAB heraus mit sim(’name’) aufrufen und die entsprechenden Bilder generieren. Definieren Sie dazu alle Parameter die SIMULINK benötigt in MATLAB.
In der Figur mit der Sprungantwort des Führungsverhaltens des Regelkreises soll zusätzlich gestrichelt mit plot(x,y,’:’) zum Vergleich die auf den Endwert 1 normierte Sprungantwort der Regelstrecke dargestellt werden. Ebenso stellen Sie die Stellgröße in einem separaten Bild dar. Beurteilen Sie den so eingestellten Regelkreis. Verändern Sie die Reglerparameter durch Variation von A, B und C so lange, bis Sie ein besseres Verhalten des Regelkreises gefunden haben. Gehen Sie wie folgt vor: Setzen Sie zunächst C=0 und stellen Sie mit A und B den Regelkreis auf ein leichtes Überschwingen ein. Dann verringern Sie das Überschwingen mit C. Ggf. müssen Sie noch A und B nachkorrigieren.
Dokumentieren Sie die Einstellwerte und die Sprungantworten. Nehmen Sie auch wieder die Stellgröße auf und vergleichen Sie sie mit der ursprünglichen Einstellung der Reglerparameter.

Lösung 1.1 Sprungantwort der Regelstrecke

Zur Lösung der Aufgabe wurde folgendes MATLAB-Script entwickelt:

%FHTW-Labor Regelungstechnik II SS2006 Versuch 1
%Entwurf und Simulation von Regelkreisen
%Norbert Schröder, Robert Lanzke

close all;      %Ausgabebereich löschen
clc;

%%%%%%%%%%%%%%%>----- Aufgabe 1.1 -----<%%%%%%%%%%%%%%%
%gegeben
V=2;
T1=7;
T2=3;
T3=0.2;
T4=0.2;
T_STOP=40;      %betrachtete Zeit in Sekunden
t=linspace(0,T_STOP,10000);     %linspace(start,stop,schrittzahl);

%Übertragungsfunktion tf (transfer function)
%allgemein: für h(s)=n(s)/d(s) schreibt man h=tf(n,d)
%Beispiel: für h=1/(1+2s) würde man h=tf([1],[2 1]) schreiben
%danach ergibt sich für ein nicht normiertes GP:
GP=(tf([V],[T1 1])*tf([1],[T2 1])*tf([1],[T3 1])*tf([1],[T4 1]))

%figure(1), der 1. step(GP,t) gibt die Formel der Übertr.fkt. aus
h=step(GP,t);   %Sprungantwort der Übertragungsfunktion mit t Schritten
hn=h/V;	    %hn – normiertes h
step(GP,t);     %zeichnet die Übertragungsfunktion
grid;
%Wertepaare (tx,hy) bei 30% und 70% suchen
index30=max(find(h<(V*0.3)));   %findet das Max. aller Werte mit h<V*0.3
index70=max(find(h<(V*0.7)));
h1=h(index30);
h2=h(index70);
t1=t(index30);
t2=t(index70);
hold on         %hold: damit stem() nicht die Grafik beseitigt
stem(t1,h1);    %stem(x,y) zeichnet Lot von (x,y) auf die x-Achse
stem(t2,h2);
hold off

%Ersatzparameter
h1=h1/V;        %Normierung für die Formel des Zweipunktverfahrens
h2=h2/V;
TG=(t2-t1)/(log((1-h1)/(1-h2))); %Zweipunktverfahren
TU=TG*log(1-h1)+t1;  %alternativ: TU=TG*log(1-h2)+t2
disp(['Die Ersatzparameter sind:']);
disp(['V=',num2str(V),' TU=',num2str(TU),'s, TG=',num2str(TG),'s'])
%Ausgabe: TU=2.7226s, TG=8.0715s

Im Quelltext sind alle benötigten Formeln und Funktionen bereits ausführlich kommentiert, daher verzichten wir auf eine weitere Erklärung.
Als Ausgabe erhalten wir folgendes:

Transfer function:
                     2
-------------------------------------------
0.84 s^4 + 8.8 s^3 + 25.04 s^2 + 10.4 s + 1
 
Die Ersatzparameter sind:
V=2 TU=2.7226s, TG=8.0715s

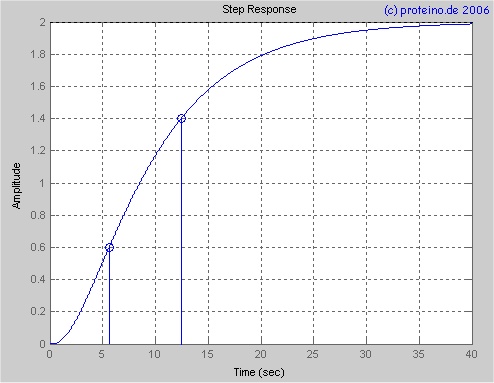
Lösung 1.2 Bestimmung der Reglerparameter, Simulation des Regelkreises

Folgender Standardregelkreis wurde erstellt: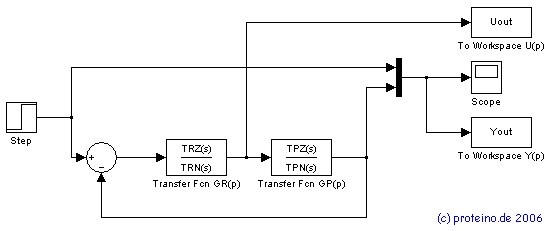

TRZ und TRN sind Zähler- und Nennerpolynom von GR
TPZ und TPN sind Zähler- und Nennerpolynom von GP

Gr(p) =TRZ/TRN
=Vr(1+(1/(pTi)+pT/(1+pTr)
=Vr(p²(TiTd+TiTr)+p(Ti+Tr)+1)/(p²TiTr+pTi)
TRZ =Vr(p²(TiTd+TiTr)+p(Ti+Tr)+1)
TRN =(p²TiTr+pTi+0)
Gp(p) =2/(0.84s^4+8.8s^3+25.04s^2+10.4s+1)
TPZ =2
TPN =0.84s^4+8.8s^3+25.04s^2+10.4s+1

Der MATLAB-Quelltext aus der Aufgabe 1.1 wurde wie folgt erweitert:

%%%%%%%%%%%%%%%>----- Aufgabe 1.2 -----<%%%%%%%%%%%%%%%
A=1.00; B=0.66; C=0.167; %A-Verstärkungsfaktor, B=I-Anteil, C=Dämpfungsfaktor
VR=A/V; TS=TU+TG; TI=B*TS; TD=C*TS; TR=0.3*TD;
TRZ=VR*[TI*TR+TI*TD TI+TR 1];    %GR(p)=VR(1+(1/pT1)+(pTD/(1+pTr)))
TRN=[TR*TI TI 0];
TPZ=[2];
TPN=[0.84 8.8 25.04 10.4 1];
sim('Labor1_2');%Simulink-Datei öffnen
figure(2)
plot(t,hn,':b'); %auf 1 normierte Sprungantwort der Regelstrecke
hold on
plot(tout,Yout,'g'); %Sprungantwort des Führungsverhaltens ohne Optmierung
Uout_h=Uout;    % Stellgröße zwischenspeichern
tout_h=tout;
A=4.1; B=0.930; C=0.160; %optmierte Parameter
%A=2.80; B=0.90; C=0.135; %schwächer opt. Par. - dafür kein Überschwingen
VR=A/V; TS=TU+TG; TI=B*TS; TD=C*TS; TR=0.3*TD;
TRZ=VR*[TI*TR+TI*TD TI+TR 1];
TRN=[TR*TI TI 0];
sim('Labor1_2');
plot(tout,Yout,'r'); %Sprungantwort des Führungsverhaltens mit Optimierung
grid;
legend('ohne Regler','Regler unoptimiert','Regler optimiert','Location','SouthEast')
hold off
figure(3);
hold on
plot(tout_h,Uout_h,':g');
plot(tout,Uout,'r');
legend('unoptimierte Stellgöße','optimierte Stellgröße');
hold off

Zu Beginn sieht man die vorgegebenen Parameter sowie die benötigten Formeln. Mit dem Aufruf von sim('mdl-file'); wird die Simulink-Simulation durchgeführt, die ungeregelte Sprungantwort und das Ergebnis werden anschließend geplotet. Für die spätere Vergleichsausgabe der Stellgröße sichern wir noch die Arrays Uout und tout. Danach kommt die Simulation und Ausgabe mit den optimierten Parametern analog zum ersten plot. Die letzten Zeilen dienen der Ausgabe der Grafik für die Stellgrößen.

Als Ergebnis werden nunmehr zusätzlich zu den unter 1.1 aufgeführten Dingen zwei weitere Grafiken (figure(2) und figure(3)) ausgegeben. Erstere zeigt die Sprungantwort der Regelstrecke sowie die Sprungantworten der geregelten Strecke mit und ohne Optmierung. In der Legende machte MATLAB hierbei einen Schönheitsfehler, den wir nicht beseitigt bekamen – die untere Linie (Regler optimiert) müßte in rot dargestellt werden.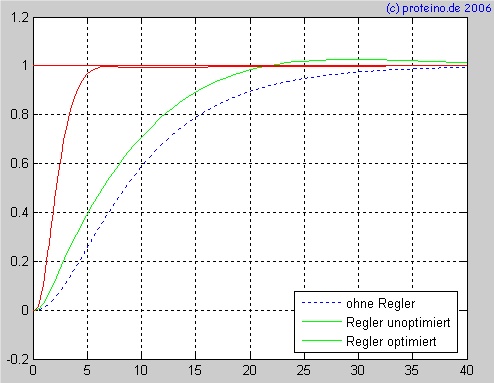

Offensichtlich ist die Sprungantwort bereits ohne unoptimierten Regler deutlich besser, als ungeregelt, zeigt dafür jedoch deutlich ein Überschwingen. Eine kontinuierliche manuelle (und zeitaufwendige) Optimierung der Reglerparameter A, B und C führte zu einer vergleichsweise bedeutend schnelleren Regelung mit nur minimalem Überschwingen (ca. 1-2%). Eine weitere Optimierung kann durch schrittweise Vergrößerung der über A eingestellten Verstärkung und entsprechende Anpassung der Parameter B und C. Bei B handelt es sich um den I-Anteil des PID-T1-Reglers, mit steigendem B wird die Anstiegszeit verringert und die Einschwingzeit vergrößert. Der Parameter C steht für den D-Anteil des Reglers, mit steigendem C wird die Anstiegszeit leicht vergrößert, dafür verringert sich jedoch das Überschwingen. Durch geeignete Variation der Parameter mit Vergleichsgrafiken (entsprechender plot in MATLAB) kann man somit manuell die Optmierung durchführen. In diesem Fall haben wir jedoch so weit optimiert, dass eine weitere Verbesserung höchstens marginale und in der Grafik kaum sichtbare Verbesserungen bringen dürfte. Lediglich bei Akzeptanz eines stärkeren Überschwingens ist ein nochmals deutlich schnellerer PID-T1-Regelkreis realisierbar.

Die 3. Grafik zeigt die Stellgrößen für den vorgegebenen sowie den optimierten Regler: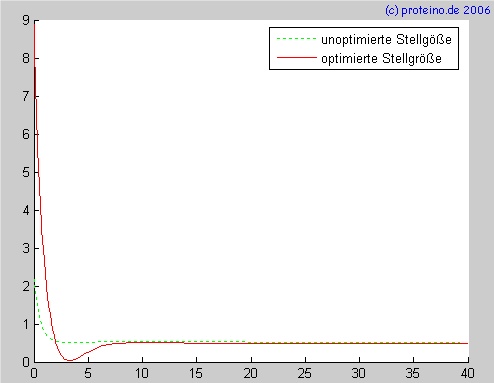

Aus dieser Grafik ist ersichtlich, dass die Optmierung schneller den Endwert (in Höhe der roten Linie rechts unten) erreicht. Deutlich sichtbar ist auch der Punkt, an dem die Sprungantwort vom sehr steilen Anstieg aus in einen flacheren übergeht, ebenso ist das Überschwingen mit der Nachregelung in der Stellgröße im Bereich von etwa 8-14 Sekunden sichtbar.

Autoren: Norbert Schröder, Robert Lanzke