Upline: Infos & Dokus Elektronik Regelungstechnik

Untersuchungen an Systemen - Systemeigenschaften

Es handelt sich bei diesem Dokument um ein Labor-Protokoll des Faches Regelungstechnik 1 im Studiengang Informationstechnik Vernetzte Systeme an der FHTW Berlin im Wintersemester 2006/07 bei Professor Dlabka.

Systemeigenschaften - Untersuchungen an Systemen

In diesem Laborversuch sollen Systeme im Hinblick auf Ihre Eigenschaften untersucht werden und unbekannte Systeme an Hand ihres Verhaltens klassifiziert werden. Für die notwendigen Berechnungen und das Zeichnen der Übertragungsfunktionen bzw. Bodediagramme wird MatLab 7 verwendet.

1 Kettenschaltung von Systemen

Es soll die Kettenschaltung gleichartiger Systeme untersucht werden. Jedes der Teilsysteme ist durch die Übertragungsfunktion G(p)=1/(1+pT) mit T=0.1s gegeben. Es sollen jeweils für 2-5 sowie 10 verkettete Teilsysteme folgende Aufgaben bearbeitet werden:

Übertragungsfunktion, Verstärkung, Systemtyp bestimmen
Bodediagramm, Erklärung des Verlaufs der Diagramme (alle 5 in einem)
Sprungantwort (zusammengefaßt für alle 5 Funktionen)

Die Übertragungsfunktion einer Verkettung von Teilsystemen ergibt sich aus der Faltung der Übertragungsfunktionen der Teilsysteme im Zeitbereich. Da in dieser Aufgabe jedes der Teilsysteme identisch ist, ergibt sich als Ergebnis eine entsprechende Potenzierung im Frequenzbereich.
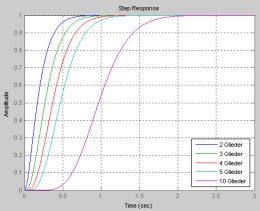
Als Systemtyp läßt sich ein P-T1-Glied (Tiefpaß 1. Ordnung) erkennen, bei dem die Verstärkung 1 beträgt. Weitere Informationen zum P-T1-Glied (Polstelle bei -1/T, keine Nullstelle, Knickkreisfrequenz ?=1/T usw.) finden sich in jeder Grundgliederübersicht.

In MatLab definiert man die Übertragungsfunktion mittels tf (transfer function) wie folgt:

GP=(tf([1],[T1 1]));

Mittels des Befehls step kann die Übertragungsfunktion grafisch dargestellt werden. Hierbei können auch gleich mehrere Übertragungsfunktionen gleichzeitig in ein Diagramm ausgegeben werden. Als letzten Parameter benötigt step eine (dem Quelltext entnehmbare) Definition der Schrittanzahl und des zu betrachtenden Zeitraums, hier t. Um die gewünschten Sprungantworten der 5 Übertragungsfunktionen auszugeben, schreibt man dann folgende Zeile:

step(GP^2,GP^3,GP^4,GP^5,GP^10,t);

In der nebenstehenden Grafik ist deutlich zu erkennen, dass sich die Anstiegszeit mit jedem zusätzlichen P-T1-Glied etwa im gleichen Verhältnis vergrößert. Es ist deutlich eine gewisse Ähnlichkeit zu erkennen, wobei der Anstieg mit jedem weiteren Glied flacher wird. Im Bereich zwischen 30% und 70% werden die entsprechenden Amplituden nahezu als Vielfaches ersichtlich. So erreichen 2 Glieder die 70% bei knapp 0.25s, 10 Glieder sind nach ca. 1.4s bei 70% der gegen 1 strebenden Amplitude angekommen. Auch wenn aus der Grafik nicht die exakten Werte abgelesen werden können und wir diese nicht extra berechnet haben, so ist die Näherung mit 0,25/2*10 rund 1.4 dennoch ersichtlich.

Die Bodediagramme lassen sich entsprechend mit dem Befehl bode wie folgt erstellen:

bode(GP^2,GP^3,GP^4,GP^5,GP^10);

Auch im Bodediagramm läßt sich die Analogie zwischen den einzelnen Graphen erkennen. Jedes P-T1-Glied bewirkt eine Phasenverschiebung um -90°, daher sieht man z.B. bei 2 Gliedern insg. -180° und bei 10 Gliedern -900°. Auch der Betrag ändert sich entsprechend und fällt wie von der Beschreibung dieses Grundgliedes bekannt mit 20dB/Dekade je Teilsystem, also für 5 verkettete P-T1-Glieder mit -100dB/Dekade ab.

Bodediagramm zur Kettenschaltung von PT-1-Gliedern

Nachfolgend der Sourcecode des MatLab-m-Files zu dieser Teilaufgabe.

%FHTW-Labor Regelungstechnik I WS2006/07 Versuch 1
%Entwurf und Simulation von Regelkreisen
%Norbert Schröder, Sebastian Buschko

close all;      %Ausgabebereich löschen
clc;

%%%%%%%%%%%%%%%>----- Aufgabe 3.1 -----<%%%%%%%%%%%%%%%
%gegeben
T1=0.1;

%Übertragungsfunktion tf (transfer function)
%allgemein: für h(s)=n(s)/d(s) schreibt man h=tf(n,d)
%Beispiel: für h=1/(1+2s) würde man h=tf([1],[2 1]) schreiben
%danach ergibt sich für ein nicht normiertes GP:
GP=(tf([1],[T1 1]));
T_STOP=3;      %betrachtete Zeit in Sekunden
t=linspace(0,T_STOP,2000);     %linspace(start,stop,schrittzahl);
hold on;
step(GP^2,GP^3,GP^4,GP^5,GP^10,t);     %zeichnet die Übertragungsfunktionen
legend('2 Glieder','3 Glieder','4 Glieder','5 Glieder','10 Glieder',...
'Location','SouthEast');
hold off;
grid;

figure(2); % step(GP,t) ohen ";" gibt die Formel der Übertr.fkt. aus
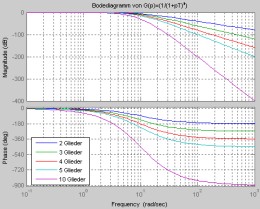
bode(GP^2,GP^3,GP^4,GP^5,GP^10)
grid;
title('Bodediagramm von G(p)=(1/(1+pT)^n)');
legend('2 Glieder','3 Glieder','4 Glieder','5 Glieder','10 Glieder',...
'Location','SouthWest');

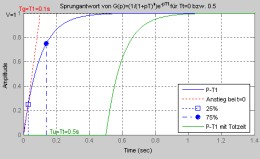
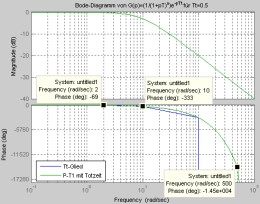
2 Bestimmung von Ersatzparametern

Da vorgegebene Systeme oft durch vereinfachte Systeme mit möglichst ähnlichem Verhalten abgebildet werden müssen, gibt es verschiedene Verfahren hierfür. Eines davon ersetzt ein System höherer Ordnung durch ein Verzögerungsglied erster Ordnung mit einer Totzeit (P-T1-Glied+Tt-Glied). Die Übertragungsfunktion dafür lautet:
G_ers(p)=V/(1+pT_G)e^-pTu
Folgende Aufgaben sind hierbei zu bearbeiten:

Formel der Sprungantwort mit Sprunghöhe 1 (Einheitsgröße) im Zeitbereich per Verschiebungssatz der Laplace-Transformation
Zeichnen der Sprungantwort mit Angabe von Zeitkonstante, Totzeit, Verstärkung und Bodediagramm mit Knickkreisfrequenz, Phase bei der Knickkreisfrequenz und der Phase der reziproken Totzeit
Herleitung der Formeln für T_G und T_U aus 1.
Bestimmung der Ersatzparameter T_G und T_U (bei 25% unbd 75%) für Kettenschaltung mit 5 bzw. 10 P-T1-Gliedern, tabellarische Angabe mit T_S=T_G+T_U und T_U/T_G
Vergleich der Ersatzübertragungsfunktion mit der originalen Übertragungsfunktion

Wie sich bereits aus der Einleitung zu dieser Aufgabe erkennen läßt, besteht die Übertragungsfunktion aus 2 Teilen, einem P-T1-Glied und einem Totzeitglied. Weiterhin wird am Eingang des Systems die Sprungfunktion U(p)=1/p angelegt. Damit er gibt sich
Y(p) = U(p) G(p)
Y(p) = V (1 / (p(1+pT_G))) e^-pTu mit V=1 (Sprunghöhe)

Die Rücktransformation in den Zeitbereich ergibt:
1 / (p(1+pT_G)) <--> 1-e^-t/Tg mit t:= t-T_U (lt. Bartsch, Kleine Formelsammlung der Mathematik)
e^-pTu <--> δ(t-T_U) (Diracimpuls, Verschiebungssatz der Laplace-Transformation)

Da nach dem Verschiebungssatz für die Laplace-Transformierten keine Faltung notwendig ist, ergibt sich als Sprungantwort:
y(t) = (1-e^-(t-Tu)/Tg) δ(t-T_U)

Für die unter 4. geforderte Verkettung von 5 bzw. 10 P-T1-Gliedern wäre eine Faltung im Zeitbereich erforderlich. Die Übertragungsfunktion für 5 Glieder sieht wie folgt aus:
G(p) = V^5 / (p^5 + 5p^4 + 10p³ + 10p² + 5p + 1)
Da die Berechnung der Formel der Sprungantwort für die Verkettung nicht gefordert ist, lassen wir die für 10 Glieder weg. MatLab erledigt die grafische Darstellung mittels der entsprechenden Übertragungsfunktionen an gegebener Stelle.

Die für T_U und T_G verwendeten Werte haben wir, da nichts vorgegeben war, willkürlich gewählt. Für T_G haben wir die im 1. Teil bereits verwendete Zeit von 0.1s erneut verwendet, welche sich auch im anfänglichen Anstieg (im rechten Bild rot gestrichelt) der Sprungantwort eines reinen P-T1-Gliedes ohne Totzeit wiederfindet. Den anderen Zeit-Parameter, also die Verzögerung (Totzeit), haben wir mit T_U=T_t=0.5s (grüne Linie mit Amplitude 0) gewählt. Die Verstärkung 1 ist aus der max. Amplitude ersichtlich. Testweise sind in der Grafik die Punkte zur Ermittlung von Ersatzparametern bei 25% und 75% integriert, was bei einem einzelnen P-T1-Glied an sich jedoch wenig Sinn macht.

Sprungantwort P-T1-Glied mit Totzeit (Tt-Glied)

Im Bodediagramm (Grafik rechts) ist mit blau das reine T_t-Glied eingezeichnet, welches ab 100Hz im Frequenzbereich eine Instabilität offenbart. Die extrem fallende Flanke wird durch die Kombination mit dem P-T1-Glied in leicht abgeschwächter Form als Knickkreisfrequenz ab 500Hz (Phase -1.45*10⁴°) sichtbar. Daraus folgt, dass die gesuchten Ersatzregler für die Verkettungen ebenfalls nicht für hohe Frequenzen geeignet sein werden. Für das P-T1-Glied wird eine Knickkreisfrequenz von 1/T angeben, was in unserem Fall die zusätzliche Knickfrequenz von 1/0.1s=10Hz ergibt. Bei 10Hz ist die Phase -333°. Die reziproke Totzeit liegt bei 1/0.5s=2Hz und einer Phase von -69°. Die Betragsfunktion im Bodediagramm für das zeitverzögerte P-T1-Glied ist wieder mit 20dB je Dekade fallend, also P-T1-typisch.

Bodediagramm P-T1-Glied mit Totzeit (Tt-Glied)

Herleitung der allgemeinen Formeln für die Ersatzparameter
Die Ersatzparameter ergeben sich aus den Punkten A(t1,x1) bei 25% der max. Amplitude und B(t2,x2) bei 75% der max. Amplitude.
y(t-T_U) = V(1-e^-(t-Tu)/Tg) mit V=x_~
x_1,2 = x_~(1-e^{-(t1,2-Tu)/Tg})

Fortsetzung folgt ... ;)